Generate embeddings from mesh

In this example, we show how to derive an embedding which approximates the kernel matrix of geodesic distances on a given mesh. This technique is useful when trying to align distributions with a large number of points. Indeed, the kernel matrix of pairwise distances won’t fit in memory, but an embedding computed in the right dimension can probably estimate it.

import gdist
import matplotlib.pyplot as plt
import numpy as np
import torch

from fugw.scripts import lmds
from nilearn import datasets, surface

Here, we will compute the exact geodesic distances from each vertex to a random sample of n_landmarks vertices. The derived embedding will be in dimension k.

torch.manual_seed(0)

n_landmarks = 100
k = 3

Let us load a pre-computed mesh and have a look at it first

fsaverage3 = datasets.fetch_surf_fsaverage(mesh="fsaverage3")
coordinates, triangles = surface.load_surf_mesh(fsaverage3.sphere_left)
coordinates.shape

Added README.md to /github/home/nilearn_data


Dataset created in /github/home/nilearn_data/fsaverage3

Downloading data from https://osf.io/azhdf/download ...
 ...done. (3 seconds, 0 min)
Extracting data from /github/home/nilearn_data/fsaverage3/472ead7320dbd53fb2ec42e05f1bb6bf/download..... done.

(642, 3)

fig = plt.figure(figsize=(5, 5))
ax = fig.add_subplot(projection="3d")
ax.plot_trisurf(
    coordinates[:, 0],
    coordinates[:, 1],
    coordinates[:, 2],
    triangles=triangles,
)
plt.show()

Now, let’s compute the embedding! This computation is easy to parallelize.

X = lmds.compute_lmds_mesh(
    coordinates,
    triangles,
    n_landmarks=n_landmarks,
    k=k,
    n_jobs=2,
    verbose=True,
)

  100% Geodesic distances (landmarks) ━━━━━━━━━━━━━━━━ 100/100 0:00:02 < 0:00:00
/github/workspace/src/fugw/scripts/lmds.py:175: UserWarning:

A might not be centered (1.8671875 > 0.001)

It should have the correct size

assert X.shape == (coordinates.shape[0], k)

We can actually have a peek at the computed embedding:

fig = plt.figure(figsize=(5, 5))
ax = fig.add_subplot(projection="3d")
ax.set_title("Embedding approximating kernel matrix")
ax.scatter(
    X[:, 0],
    X[:, 1],
    X[:, 2],
    s=15,
)
plt.show()

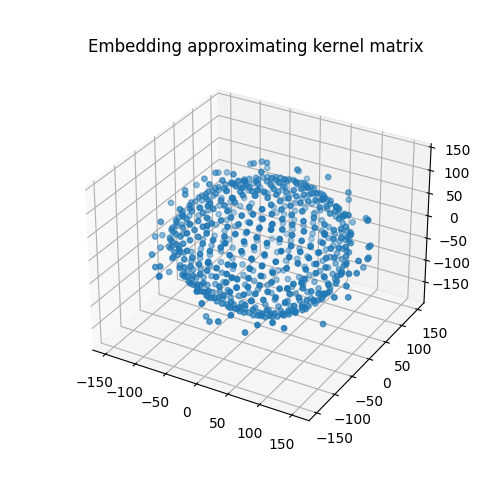
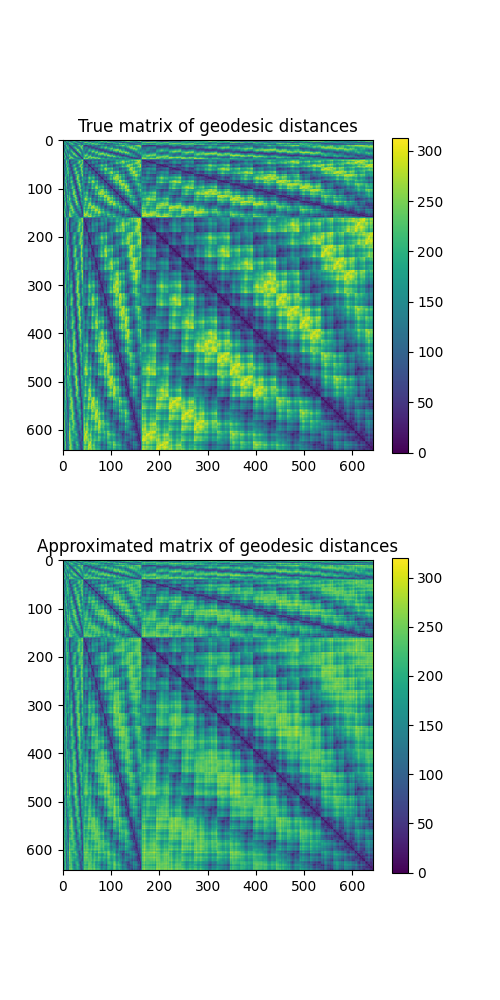
Finally, we check that the exact matrix of geodesic distances between pairs of vertices of the mesh is well approximated by the kernel matrix derived from the embeddings:

fig = plt.figure(figsize=(5, 10))

ax = fig.add_subplot(211)
ax.set_title("True matrix of geodesic distances")
true_kernel_matrix = gdist.local_gdist_matrix(
    coordinates.astype(np.float64),
    triangles.astype(np.int32),
).toarray()
im = ax.imshow(true_kernel_matrix)
plt.colorbar(im, ax=ax, shrink=0.9)

ax = fig.add_subplot(212)
ax.set_title("Approximated matrix of geodesic distances")
approximated_kernel_matrix = torch.cdist(X, X)
im = ax.imshow(approximated_kernel_matrix)
plt.colorbar(im, ax=ax, shrink=0.9)

plt.show()

Estimated memory usage: 133 MB