Note
Go to the end to download the full example code.
Monitor the Pearson correlation during training with callbacks#
In this example, we use a callback function to monitor the Pearson correlation between transformed and target features at each iteration of the block-coordinate descent (BCD) algorithm. This can be useful to detect numerical errors, or to check that the mapping is not over-fitting training data.
from functools import partial
import matplotlib.pyplot as plt
import numpy as np
import torch
import time
from nilearn import datasets, image
from rich.console import Console
from scipy.spatial import distance_matrix
from scipy.linalg import norm
from fugw.mappings import FUGW
from fugw.utils import _make_tensor
We first fetch 6 contrasts for each subject from the localizer dataset. We use 3 contrasts for training and 3 contrasts for validation.
n_subjects = 2
contrasts = [
"sentence reading",
"calculation vs sentences",
"left vs right button press",
"sentence reading vs checkerboard",
"sentence listening",
"left button press",
]
n_training_contrasts = 3
brain_data = datasets.fetch_localizer_contrasts(
contrasts,
n_subjects=n_subjects,
get_anats=True,
get_masks=True,
)
source_imgs_paths = brain_data["cmaps"][0 : len(contrasts)]
target_imgs_paths = brain_data["cmaps"][len(contrasts) : 2 * len(contrasts)]
source_mask = brain_data["masks"][0]
source_im = image.load_img(source_imgs_paths)
target_im = image.load_img(target_imgs_paths)
mask = image.load_img(source_mask)
Downloading data from https://osf.io/download/5d27c4a51c5b4a001c9e75b1/ ...
...done. (2 seconds, 0 min)
Downloading data from https://osf.io/download/5d27c81645253a001c3e1f85/ ...
...done. (3 seconds, 0 min)
Downloading data from https://osf.io/download/5d27d931114a4200190452fe/ ...
...done. (2 seconds, 0 min)
Downloading data from https://osf.io/download/5d27d62e114a420017049501/ ...
...done. (2 seconds, 0 min)
Downloading data from https://osf.io/download/5d27cdcaa26b340018084b30/ ...
...done. (1 seconds, 0 min)
Downloading data from https://osf.io/download/5d27d80c114a420016058f7d/ ...
...done. (1 seconds, 0 min)
We then downsample the images by 5 to reduce the computational cost.
SCALE_FACTOR = 5
resized_source_affine = source_im.affine.copy() * SCALE_FACTOR
resized_target_affine = target_im.affine.copy() * SCALE_FACTOR
source_im_resized = image.resample_img(source_im, resized_source_affine)
target_im_resized = image.resample_img(target_im, resized_target_affine)
mask_resized = image.resample_img(mask, resized_source_affine)
source_maps = np.nan_to_num(source_im_resized.get_fdata())
target_maps = np.nan_to_num(target_im_resized.get_fdata())
segmentation = mask_resized.get_fdata()
coordinates = np.argwhere(segmentation > 0)
source_features = source_maps[
coordinates[:, 0], coordinates[:, 1], coordinates[:, 2]
].T
target_features = target_maps[
coordinates[:, 0], coordinates[:, 1], coordinates[:, 2]
].T
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:664: RuntimeWarning:
NaNs or infinite values are present in the data passed to resample. This is a bad thing as they make resampling ill-defined and much slower.
/usr/local/lib/python3.8/site-packages/nilearn/image/resampling.py:293: UserWarning:
Resampling binary images with continuous or linear interpolation. This might lead to unexpected results. You might consider using nearest interpolation instead.
We then compute the distance matrix between voxel coordinates.
source_geometry = distance_matrix(coordinates, coordinates)
target_geometry = source_geometry.copy()
In order to avoid numerical errors when fitting the mapping, we normalize all feature and geometry arrays.
source_features_normalized = source_features / np.linalg.norm(
source_features, axis=1
).reshape(-1, 1)
target_features_normalized = target_features / np.linalg.norm(
target_features, axis=1
).reshape(-1, 1)
source_geometry_normalized = source_geometry / np.max(source_geometry)
target_geometry_normalized = target_geometry / np.max(target_geometry)
We first define a function to compute the Pearson correlation between two tensors. Such function is not available in PyTorch, but it is easy to implement.
def pearson_corr(a, b, plan):
"""
Compute the Pearson correlation between transformed
source features and target features.
"""
if torch.is_tensor(a):
x = a.detach().cpu().numpy()
elif isinstance(a, np.ndarray):
x = a
elif isinstance(a, list):
x = np.array(a)
else:
raise ValueError("a must be a list, np.ndarray or torch.Tensor")
if torch.is_tensor(b):
y = b.detach().cpu().numpy()
elif isinstance(b, np.ndarray):
y = b
elif isinstance(b, list):
y = np.array(b)
else:
raise ValueError("b must be a list, np.ndarray or torch.Tensor")
# Compute the transformed features
x_transformed = (
(plan.T @ x.T / plan.sum(dim=0).reshape(-1, 1)).T.detach().cpu()
)
return pearson_r(x_transformed, y)
def pearson_r(a, b):
"""Compute Pearson correlation between x and y.
Compute Pearson correlation between 2d arrays x and y
along the samples axis.
Adapted from scipy.stats.pearsonr.
Parameters
----------
a: np.ndarray of size (n_samples, n_features)
b: np.ndarray of size (n_samples, n_features)
Returns
-------
r: np.ndarray of size (n_samples,)
"""
if torch.is_tensor(a):
x = a.detach().cpu().numpy()
elif isinstance(a, np.ndarray):
x = a
elif isinstance(a, list):
x = np.array(a)
else:
raise ValueError("a must be a list, np.ndarray or torch.Tensor")
if torch.is_tensor(b):
y = b.detach().cpu().numpy()
elif isinstance(b, np.ndarray):
y = b
elif isinstance(b, list):
y = np.array(b)
else:
raise ValueError("b must be a list, np.ndarray or torch.Tensor")
dtype = type(1.0 + x[0, 0] + y[0, 0])
xmean = x.mean(axis=1, dtype=dtype)
ymean = y.mean(axis=1, dtype=dtype)
# By using `astype(dtype)`, we ensure that the intermediate calculations
# use at least 64 bit floating point.
xm = x.astype(dtype) - xmean[:, np.newaxis]
ym = y.astype(dtype) - ymean[:, np.newaxis]
# Unlike np.linalg.norm or the expression sqrt((xm*xm).sum()),
# scipy.linalg.norm(xm) does not overflow if xm is, for example,
# [-5e210, 5e210, 3e200, -3e200]
normxm = norm(xm, axis=1)
normym = norm(ym, axis=1)
r = np.sum(
(xm / normxm[:, np.newaxis]) * (ym / normym[:, np.newaxis]), axis=1
)
return r
We then define a callback function that computes the Pearson correlation between transformed features and target features at each BCD iteration.
# Initialize the transport plan with ones and normalize it
init_plan = torch.ones(
(
source_features_normalized.shape[1],
source_features_normalized.shape[1],
)
)
init_plan_normalized = init_plan / init_plan.sum()
# Initialize the list of Pearson correlations by fitting
# source features with the initial plan
corr_bcd_steps = [
pearson_corr(
source_features_normalized[n_training_contrasts:],
target_features_normalized[n_training_contrasts:],
init_plan_normalized,
)
]
def correlation_callback(
locals,
source_features=None,
target_features=None,
device=torch.device("cpu"),
):
console = Console()
# Get current transport plan and tensorize features
pi = locals["pi"]
source_features_tensor = _make_tensor(source_features, device)
target_features_tensor = _make_tensor(target_features, device)
# Compute the Pearson correlation and append it to the list
corr = pearson_corr(source_features_tensor, target_features_tensor, pi)
corr_bcd_steps.append(corr)
console.log("Pearson correlation: ", corr)
We now fit the mapping using the sinkhorn solver and 5 BCD iterations.
device = "cpu"
start_time = time.time()
mapping = FUGW(alpha=0.5, rho=1, eps=1e-4)
_ = mapping.fit(
source_features=source_features_normalized[:n_training_contrasts],
target_features=target_features_normalized[:n_training_contrasts],
source_geometry=source_geometry_normalized,
target_geometry=target_geometry_normalized,
source_features_val=source_features_normalized[n_training_contrasts:],
target_features_val=target_features_normalized[n_training_contrasts:],
init_plan=init_plan_normalized,
solver="sinkhorn",
solver_params={
"nits_bcd": 5,
},
callback_bcd=partial(
correlation_callback,
source_features=source_features_normalized[n_training_contrasts:],
target_features=target_features_normalized[n_training_contrasts:],
device=device,
),
verbose=True,
device=device,
)
total_time = time.time() - start_time
[14:39:47] Validation data for anatomical kernels is not provided. dense.py:226
Using training data instead.
[14:39:52] BCD step 1/5 FUGW loss: 0.02471640333533287 dense.py:568
Validation loss: 0.02700098603963852
[14:39:52] Pearson correlation: [0.38212429 plot_1_pearson_correlation.py:237
0.2964243 0.26874193]
[14:40:02] BCD step 2/5 FUGW loss: 0.006555820349603891 dense.py:568
Validation loss: 0.007569685112684965
[14:40:02] Pearson correlation: [0.31391999 plot_1_pearson_correlation.py:237
0.34292094 0.32424131]
[14:40:11] BCD step 3/5 FUGW loss: 0.006002967711538076 dense.py:568
Validation loss: 0.006645429879426956
[14:40:11] Pearson correlation: [0.33015294 plot_1_pearson_correlation.py:237
0.33416723 0.31084012]
[14:40:20] BCD step 4/5 FUGW loss: 0.005948252975940704 dense.py:568
Validation loss: 0.006552045699208975
[14:40:20] Pearson correlation: [0.32666147 plot_1_pearson_correlation.py:237
0.32980771 0.29679679]
[14:40:29] BCD step 5/5 FUGW loss: 0.005936595611274242 dense.py:568
Validation loss: 0.006547404453158379
[14:40:29] Pearson correlation: [0.32642125 plot_1_pearson_correlation.py:237
0.33017425 0.29350384]
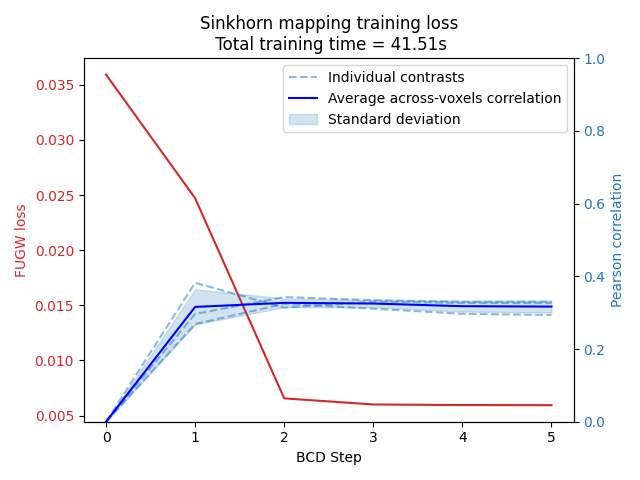
The Pearson correlation relative to each validation contrast and training loss evolution are then plotted for each BCD iteration. Notice how the average across-voxel correlation spikes right after the first BCD iteration.
corr_bcd_steps = np.array(corr_bcd_steps)
mean_corr = np.mean(corr_bcd_steps, axis=1)
std_corr = np.std(corr_bcd_steps, axis=1)
fig, ax1 = plt.subplots()
color = "tab:red"
ax1.set_xlabel("BCD Step")
ax1.set_ylabel("FUGW loss", color=color)
ax1.plot(mapping.loss_steps, mapping.loss["total"], color=color)
ax1.tick_params(axis="y", labelcolor=color)
ax2 = ax1.twinx() # instantiate a second axes that shares the same x-axis
color = "tab:blue"
ax2.set_ylabel("Pearson correlation", color=color)
for i in range(len(source_features_normalized[n_training_contrasts:])):
ax2.plot(
mapping.loss_steps[: len(corr_bcd_steps)],
corr_bcd_steps[:, i],
color=color,
alpha=0.5,
linestyle="dashed",
label="Individual contrasts" if i == 0 else None,
)
ax2.set_label("Pearson correlation")
ax2.plot(
mapping.loss_steps[: len(corr_bcd_steps)],
mean_corr,
color="blue",
label="Average across-voxels correlation",
)
ax2.fill_between(
mapping.loss_steps[: len(corr_bcd_steps)],
mean_corr - std_corr,
mean_corr + std_corr,
color=color,
alpha=0.2,
label="Standard deviation",
)
ax2.set_ylim(0, 1)
ax2.tick_params(axis="y", labelcolor=color)
plt.title(
f"Sinkhorn mapping training loss\n Total training time = {total_time:.2f}s"
)
fig.tight_layout()
plt.legend()
plt.show()
Total running time of the script: (0 minutes 56.407 seconds)
Estimated memory usage: 65 MB